*本記事は旧TechblogからCOLORSに統合した記事です。
目次
・はじめに
・自己紹介
・仮説と検証方針
・重回帰分析について
・分析結果
・まとめ
はじめに
こんにちは。AIFのT.Oです。
2020年5月現在、コロナウィルスにより世界的に自粛モードです。
今回は人口流入がコロナウィルスの新規感染者数に影響を与えるといえるのか、統計的に調べてみました。
自己紹介
大学では数学をメインに学んでいました。当時は数学のなかでも統計は苦手で、プログラミングも苦手でした。しかしいまは、データサイエンスにかかわる中で統計の面白さやプログラミングの楽しさに触れています。
仮説と検定方針
〇分析するにあたって
まずは「仮説」を立てます。仮説とは、例えば「身長が高い人の親もまた身長が高いのではないか」、「数学が得意な人はプログラミングも得意なのではないか」といった“実際正しいかどうかはわからないけども、成り立っているとおく前提”のことです。
仮説のままでは正しいかわからないので、それを検証します。
仮説検証の方法の一つとして、「検定」があります。検定をおこなうことで、現実に起きた現象が偶然により起きたものなのか、偶然というには無理がある、つまり何らかの意味があると判断することができます。
例えば、10人に痩せる薬を服用してもらったとしましょう。1週間後、服用の前後で平均体重を比較したところ、1kg下がっていたとします。これは薬に効果があったといえるのか。仮説検定することでわかります。
〇仮説
潜伏期間を14日として、
① 14日前の人口流入
→人口流入量が多ければ多いほど新規感染者数が増えると推測。
② 過去14日間の累計新規感染者数
→過去14日間に発症した人は14日前時点で保菌者として活動していたと推測。
の2つが新規感染者数に強く影響を与えると考えます。
〇データ
・対象地域:東京都
・対象期間:2020/03/19~2020/04/30
・Agoop社より、お台場・歌舞伎町・渋谷センター街の人口流入データを使用。Agoop社HP URL https://www.agoop.co.jp/floating-population/
・東京都公式HPより、コロナウィルス感染者データを使用。
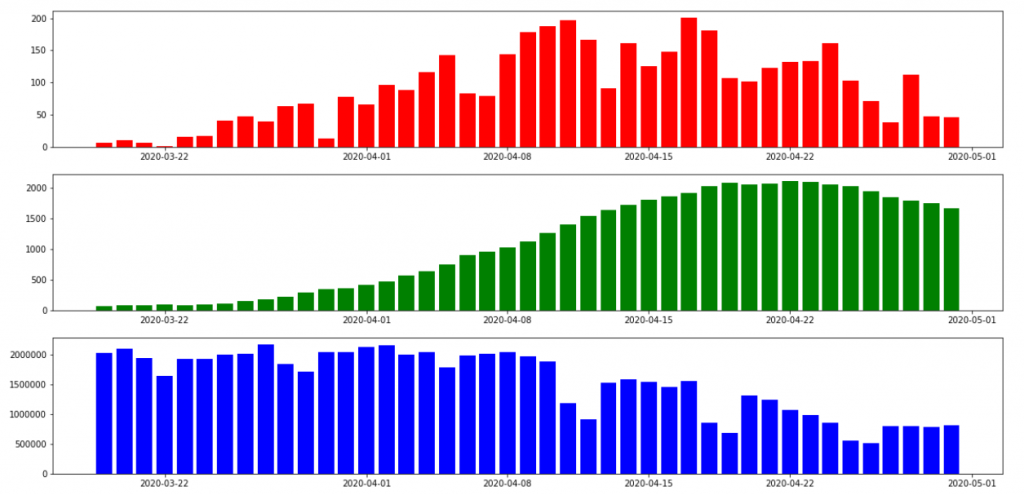
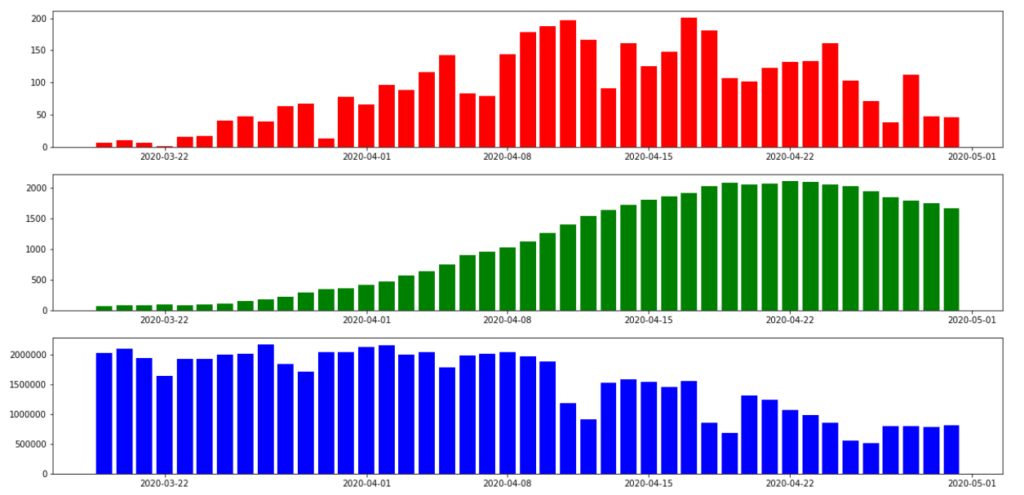
〇データの推移
上から、新規感染者数、累積感染者数、人口流入の推移です。
重回帰分析について
〇回帰モデルとは
回帰モデルとはざっくり言うと「数値を予測するモデル」です。
例えば、「体重と性別から身長を予測する回帰モデル」などが考えられます。それに対してカテゴリを予測するモデルを分類モデルといいます。「身長、体重から性別を予測する分類モデル」などが考えられます。
回帰モデルも分類モデルも「教師あり学習モデル」と呼ばれます。
また、予測する数値やカテゴリを目的変数や応答変数、予測につかう数値やカテゴリを説明変数と呼びます。
教師あり学習モデルでは、あらかじめ目的変数と説明変数がそろったデータ(教師データ)を用意して、「学習」させることで予測できるようになります。
〇重回帰分析
重回帰分析は最もシンプルな線形回帰モデルです。
イメージとしては直線や平面のような“まっすぐなもの”でモデルを表します。当然、“まっすぐなもの”で上手く表現できるとは限りませんし、予測だけに重みをおくならもっと複雑なモデルのほうが適しているかもしれませんが、重回帰分析の利点としてモデルのあてはまりの良さを決定係数という形で数値化できたり、標準偏回帰係数を通して各説明変数の影響度を定量的に比較できたりするメリットがあります。今回も、予測のためというよりは、モデルの当てはまりの良さ、説明変数の影響度を調べるために重回帰分析を選びました。
具体的には、
y:目的変数
xi:説明変数
として、目的変数を説明変数の線形和で表現します。
y=w0+w1x1+w2x2+…+wnxn
「wi」は偏回帰係数と呼ばれ、最小二乗法により求めることができます。
また、
・総変動ST…観測された目的変数の平均からのばらつき
・回帰による変動SR…重回帰モデルにより説明されるばらつき
・残差Se…重回帰モデルで説明できていないばらつき
の3つにより、モデルそのもののあてはまりの良さである
決定係数 R2…SR/ST をもとめることができます。
決定係数は説明変数が大きくなるほど大きくなる傾向があるため、異なるモデル間でもモデルの良さを比較できるように導入されたのが自由度調整済み決定係数 R*2です。
また、SRとSeを自由度でわった平均平方の比はF分布に従い、
偏回帰係数のどれかひとつでも意味のあるものがあるか検定にかけることができます。
詳細は省略しますが、各説明変数についてもt値を計算して検定をおこない、目的変数に影響を与えているといえるかを示すことができます。
分析結果
まず重回帰分析に意味があったのかというところからみていきます。

決定係数が0.5以上であることから、それなりに目的変数=新規感染者数を説明できていることがわかります。
また、F検定が有意水準5%で棄却され、p値も非常に低いことから、
説明変数2つのうち少なくとも一つの影響があることがわかります。
次に説明変数ごとに影響をみていきましょう。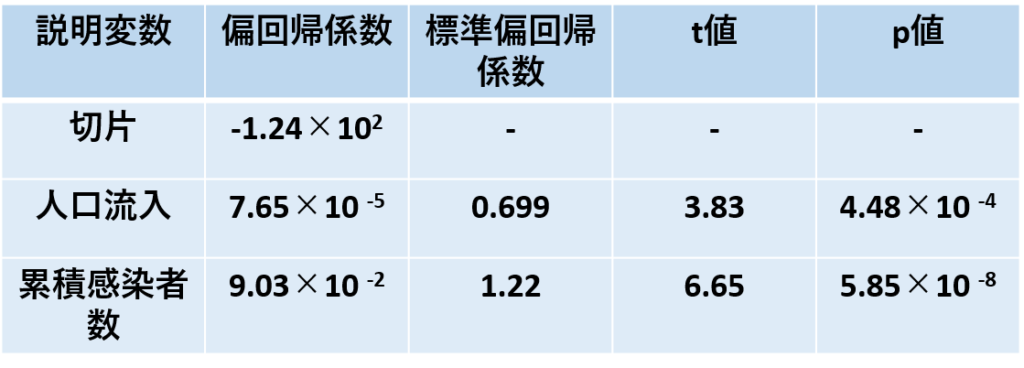
人口流入、累積感染者数ともにt値は2以上であり、
有意水準5%で棄却されるうえにp値も非常に小さいです。
よってどちらも新規感染者数に影響を与えるといえます。
また、どちらもプラスの値であるので、人口流入と累積感染者数
どちらが増えても新規感染者が増えることになります。
標準偏回帰係数を比べると、累積感染者数のほうが2倍弱影響しているといえます。
相関係数も調べてみました。
〇相関とは
相関とは、二つの量が連動している度合いです。
例えば、「家賃と部屋の広さ」は相関があります。家賃が高ければ部屋は広い傾向があるでしょうし、部屋が広ければ家賃が高い傾向があるでしょう。このようにどちらかが大きくなるともう一方も大きくなる関係を正の相関があるといいます。逆に、「家賃と築年数」はどうでしょうか。家賃が高いと築年数は少なくなる傾向があり、逆に築年数が増えれば家賃は安くなる傾向がありそうです。このようにどちらかが大きくなるともう一方は小さくなる関係を負の相関があるといいます。
また、お互いほとんど連動しない関係を無相関といいます。
相関の度合いは“相関係数”を使って定量的にあらわすことができます。相関係数は-1~1の値をとり1に近いほど正の相関が強く、逆に-1に近いほど負の相関が強いです。0付近は無相関になります。
正負関係なく絶対値で0.5~0.7程度が弱い相関、0.7~0.9がやや強い相関、0.9以上は強い相関となります(目安は人により異なります)。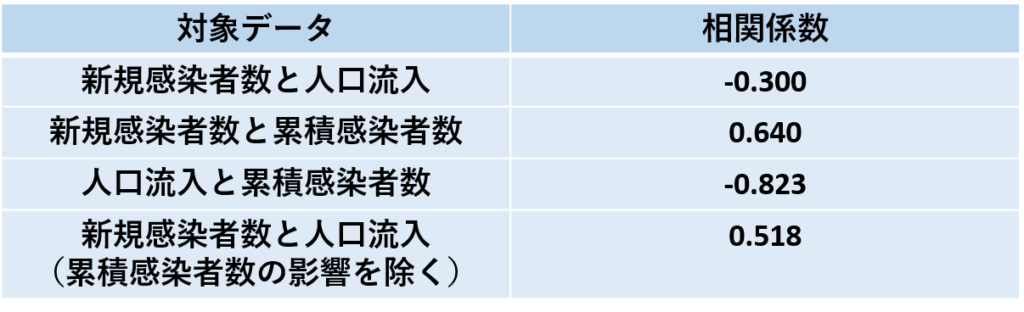
〇係数矛盾
ここで係数矛盾が生じています。重回帰分析ではプラスの寄与があるとされた人口流入が弱いマイナスの相関を示しています。そこで累積感染者数の影響を除去して偏相関係数を計算したところ、プラスの値となり、偏回帰係数と符合が一致しました。
〇多重共線性
人口流入と累積感染者数がやや強い負の相関を示しているので、多重共線性について調べてみました(通常は0.9以上の場合に疑います)。多重共線性とは説明変数同士の相関が極めて強いとき、偏回帰係数の予測が不安定になることをいいます。
今回は分散拡大係数をチェックすることによって多重共線性を考慮する必要があるか調べてみました。
その結果分散拡大係数は約3.09でした。10を超えると多重共線性を考慮する必要があるといわれていますので、今回は多重共線性を考慮しなくても大丈夫でした。
まとめ
今回は仮説モデルのもとで人口流入の増加が新規感染者数を増やすことを統計的に示すことができました。
自粛自粛とつらい時期ですが、一人一人が自制心をもつことでこの難局を乗り切れると信じています。
また、今回は仮説検証するためにシンプルな重回帰モデルを採用しましたが、予測を行うとなるとまた話は違ってきます。もっと複雑なモデルでの予測にもチャレンジできたらと思います。